Is impedance matching important?
Impedance can refer to many different things, including cable reactive impedance, cable characteristic impedance, and component input and output impedance.
Reactive Impedance
Reactive impedance is the combination of resistance, inductance and capacitance in a network (which may be a cable). Reactive impedance is a function of frequency and consists of R, XL and XC terms in combination, where XL equals wL and XC equals 1/wC (w = 2pf, f is frequency in Hz). Reactive impedance will change as a cable is lengthened. This is because it is considered a "lumped" Impedance. As the cable grows in length, R, L and C will increase and therefore XL and XC and R will increase as well. At audio frequencies, this is the primary effect. This is why minimizing cable length is always a good idea.
Characteristic Impedance
Characteristic impedance is a high-frequency phenomenon that is a function of the "distributed" R, L and C (inductance and capacitance per unit length). Characteristic impedance Z0 is calculated as (Lu/Cu)1/2 . Lu and Cu are inductance and capacitance per unit length. From the Z0 equation, you can see that Z0 is independent of the length of the cable, the frequency and the resistance. This behavior holds true only if the wavelength of the frequencies on the cable is much shorter than the transit time of a signal from one end of the cable to the other. When this is true, the characteristic impedance will stay relatively constant regardless of the length of the cable and the cable will exhibit "transmission-line-effects". In general, if an event is so fast that it completes a significant voltage transition before it is noticed at the far end of the cable, this will cause transmission-line-effects to occur. Transit times are very short for typical audio cables. For example, a 20 foot speaker cable has a transit time of around 40 nanoseconds. In order for transmission-line-effects to occur on this cable, signals at frequencies above 25MHz must be present. This is orders of magnitude higher than audio frequencies. Therefore, transmission-line-effects and characteristic impedance are definitely second-order effects on audio cables, however resonance may play more significant part than previously imagined and this relates to termination of the characteristic impedance.
Interconnects and impedance
It is often asked whether interconnects or components need to be "impedance-matched". There is no real matching with audio systems. The most important attributes for line-level RCA-type analog interconnections are:
Low driver output impedance (5-10 ohms is good)
Low interconnect capacitance (10-20pf/foot is good)Low receiver input capacitance (not usually published) Component input resistance isn't very critical, but it should probably be greater than 1K ohms. 10K-100K ohms is typical.
Speaker cable and impedance
There is no specific impedance matching between power amps, speaker cables and loudspeakers, particularly since loudspeakers represent such complex loads. The most important attributes for loudspeaker connections are:
- Low driver output impedance (.1-.3 ohms is good)
- Low speaker cable resistance and inductance
- Low speaker impedance (to get more acoustic output per amplifier watt)
Speaker cable resonance and matching Z0
Since speaker cables are generally longer and driven by high-power, sometimes high-bandwidth amplifiers, they can be prone to high-frequency resonances. If the speaker cable characteristic impedance closely matches the impedance of the loudspeaker, these resonances can be absorbed by the resistance of the speaker. In order for this to happen, however, the speaker impedance must be purely resistive and equal the cable Z0 at high frequencies. Very few speakers have this characteristic. Purely for an academic exercise, we performed some SPICE simulations of our Clarity7 speaker cable. We determined that the Z0 of the Clarity7 cable is 11 ohms. Therefore, in theory, if we connect a purely resistive 11 ohm speaker load, the resonances should dissappear. In the same spectral plot below, we show a 4.86m Clarity7 (with anti-resonant termination removed) driving a 3 ohm resistive load and an 11 ohm resistive load:
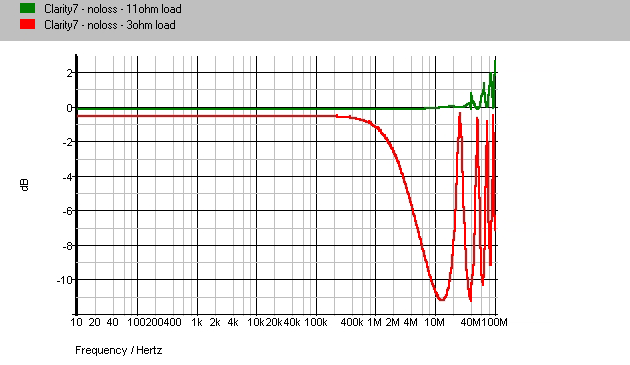
The fundamental resonant peak is obvious at 25MHz in the red curve along with a number of additional harmonic peaks (this is the 3 ohm resistive load). The green curve shows that virtually all of the resonances are smoothed-out and the power bandwidth is increased from 2.5MHz to at least 100MHz. The advantage of having a speaker that matches the cable Z0 is not that you get increased bandwidth to 100MHz. This is certainly not necessary for audio. The advantage is that the roll-off, and the phase-shift that accompanies it is completely eliminated. The frequency and phase response are ruler-flat across the audio band and beyond. In an ideal world, this would be great. In the real world, speakers are not purely resistive loads and they don't match the cable characteristic impedance, so most cables exhibit the resonance. Empirical Audio eliminates the resonance for all speaker loads with our anti-resonance terminations (see FAQ on resonance).